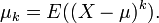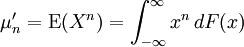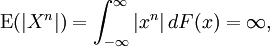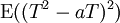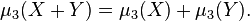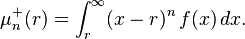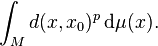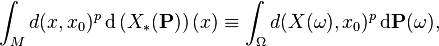理解距（数学）-白红宇

理解距（数学）

阅读量：6835 次

发布时间：2019-06-26

本文共 7138 字，大约阅读时间需要 23 分钟。

In , a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" (in a particular sense) of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by an . Other moments describe other aspects of a such as how the distribution is skewed from its mean, or peaked. The mathematical concept is closely related to the concept of in , although moment in physics is . Any distribution can be characterized by a number of features (such as the mean, the variance, the skewness, etc.), and the moments of a function describe the nature of its distribution.

The 1st moment is denoted by μ₁. The first moment of the distribution of the random variable X is the expectation operator, i.e., the (if the first moment exists).

In higher orders, the central moments (moments about the mean) are more interesting than the moments about zero. The kth , of a real-valued random variable probability distribution X, with the μ is:

$\mu_k=E((X-\mu)^k).\,$

The first central moment is thus 0. The zero-th central moment, μ₀ is one. See also .

Significance of the moments 距的重要性

The n^th moment of a real-valued continuous function f(x) of a real variable about a value c is

$\mu'_n=\int_{-\infty}^\infty (x - c)^n\,f(x)\,dx.\,\!$

It is possible to define moments for in a more general fashion than moments for real values—see . The moment of a function, without further explanation, usually refers to the above expression with c = 0.

Usually, except in the special context of the , the function f(x) will be a . The n^th moment about zero of a probability density function f(x) is the of Xⁿ and is called a raw moment or crude moment. The moments about its mean μ are called ; these describe the shape of the function, independently of .

If f is a , then the value of the integral above is called the nth moment of the . More generally, if F is a of any probability distribution, which may not have a density function, then the nth moment of the probability distribution is given by the

$\mu'_n = \operatorname{E}(X^n)=\int_{-\infty}^\infty x^n\,dF(x)\,$

where X is a that has this distribution and E the or mean.

When

$\operatorname{E}(|X^n|) = \int_{-\infty}^\infty |x^n|\,dF(x) = \infty,\,$

then the moment is said not to exist. If the nth moment about any point exists, so does (n − 1)th moment, and all lower-order moments, about every point.

Variance方差

Main article:

The second about the mean is the , the positive square root of which is the σ.

Normalized moments 正规距

The normalized nth central moment or is the nth central moment divided by σⁿ; the normalized nth central moment of x = E((x − μ)ⁿ)/σⁿ. These normalized central moments are , which represent the distribution independently of any linear change of scale.

Skewness 偏态

Main article:

The third central moment is a measure of the lopsidedness of the distribution; any symmetric distribution will have a third central moment, if defined, of zero. The normalized third central moment is called the , often γ. A distribution that is skewed to the left (the tail of the distribution is heavier on the left) will have a negative skewness. A distribution that is skewed to the right (the tail of the distribution is heavier on the right), will have a positive skewness.

For distributions that are not too different from the , the will be somewhere near μ − γσ/6; the about μ − γσ/2.

Kurtosis 峰态

Main article:

The fourth central moment is a measure of whether the distribution is tall and skinny or short and squat, compared to the normal distribution of the same variance. Since it is the expectation of a fourth power, the fourth central moment, where defined, is always non-negative; and except for a , it is always strictly positive. The fourth central moment of a normal distribution is 3σ⁴.

The κ is defined to be the normalized fourth central moment minus 3. (Equivalently, as in the next section, it is the fourth divided by the square of the variance.) Some authorities do not subtract three, but it is usually more convenient to have the normal distribution at the origin of coordinates. If a distribution has a peak at the mean and long tails, the fourth moment will be high and the kurtosis positive (leptokurtic); and conversely; thus, bounded distributions tend to have low kurtosis (platykurtic).

The kurtosis can be positive without limit, but κ must be greater than or equal to γ² − 2; equality only holds for . For unbounded skew distributions not too far from normal, κ tends to be somewhere in the area of γ² and 2γ².

The inequality can be proven by considering

$\operatorname{E} ((T^2 - aT)^2)\,$

where T = (X − μ)/σ. This is the expectation of a square, so it is non-negative whatever a is; on the other hand, it's also a in a. Its must be non-positive, which gives the required relationship.

Mixed moments 混合距

Mixed moments are moments involving multiple variables.

Some examples are , and . While there is a unique covariance, there are multiple co-skewnesses and co-kurtoses.

Higher moments 高阶距

High-order moments are moments beyond 4th-order moments. The higher the moment, the harder it is to estimate, in the sense that larger samples are required in order to obtain estimates of similar quality.^[]

Cumulants 累积距

Main article:

The first moment and the second and third unnormalized central moments are additive in the sense that if X and Y are random variables then

$\mu_1(X+Y)=\mu_1(X)+\mu_1(Y)\,$

and

$\operatorname{Var}(X+Y)=\operatorname{Var}(X) + \operatorname{Var}(Y)$

and

$\mu_3(X+Y)=\mu_3(X)+\mu_3(Y).\,$

(These can also hold for variables that satisfy weaker conditions than independence. The first always holds; if the second holds, the variables are called ).

In fact, these are the first three cumulants and all cumulants share this additivity property.

Sample moments 样本距

The moments of a population can be estimated using the sample k-th moment

$\frac{1}{n}\sum_{i = 1}^{n} X^k_i\,\!$

applied to a sample X₁,X₂,..., X_n drawn from the population.

It can be shown that the expected value of the sample moment is equal to the k-th moment of the population, if that moment exists, for any sample size n. It is thus an unbiased estimator.

Problem of moments 距的问题

The seeks characterizations of sequences { μ′_n : n = 1, 2, 3, ... } that are sequences of moments of some function f.

Partial moments 部分距/一边距

Partial moments are sometimes referred to as "one-sided moments." The nth order lower and upper partial moments with respect to a reference point r may be expressed as

$\mu_n^-(r)=\int_{-\infty}^r (r - x)^n\,f(x)\,dx,$

$\mu_n^+(r)=\int_r^\infty (x - r)^n\,f(x)\,dx.$

Partial moments are normalized by being raised to the power 1/n. The may be expressed as a ratio of a first-order upper partial moment to a normalized second-order lower partial moment.

Moments in metric spaces 矩阵空间中的距

Let (M, d) be a , and let B(M) be the on M, the generated by the d- of M. (For technical reasons, it is also convenient to assume that M is a with respect to the d.) Let 1 ≤ p ≤ +∞.

The p^th moment of a measure μ on the (M, B(M)) about a given point x₀ in M is defined to be

$\int_{M} d(x, x_{0})^{p} \, \mathrm{d} \mu (x).$

μ is said to have finite p^th moment if the p^th moment of μ about x₀ is finite for some x₀ ∈ M.

This terminology for measures carries over to random variables in the usual way: if (Ω, Σ, P) is a and X : Ω → M is a random variable, then the p^th moment of X about x₀ ∈ M is defined to be

$\int_{M} d (x, x_{0})^{p} \, \mathrm{d} \left( X_{*} (\mathbf{P}) \right) (x) \equiv \int_{\Omega} d (X(\omega), x_{0})^{p} \, \mathrm{d} \mathbf{P} (\omega),$

and X has finite p^th moment if the p^th moment of X about x₀ is finite for some x₀ ∈ M.